Optimisation de recettes via le solveur linaire

La fonction @glop.optimize() permet de calculer la recette en maximisant ou minimisant une certaine caractéristique sous certaines contraintes.

Les caractéristiques supportées sont  :

• les compositions (compo[]) ;
• les nutriments (nut[]) ;
• les coûts (cost[]) ;
• les allergènes (allergen[]) ;
• les ingrédients (ing[]).

Les objets de contraintes sont soit des caractéristiques, soit des identifiants de contraintes spéciales. Une contrainte spéciale nécessite plusieurs caractéristiques pour la définir. Actuellement, la seule implémentée est "recipeQtyUsed" qui est la somme de toutes les quantités de composants dans la recette.

Exemple

Nous partons d'un Produit Fini qui contient 3 Matières Premières.

Nous souhaitons optimiser la recette pour atteindre certaines cibles de nutriments et de quantités mises en oeuvre.

Il faut tout d'abord ajouter les colonnes "Cible d'optimisation" et "Valeur d'optimisation" sur la liste Composition et sur la liste Nutriments :

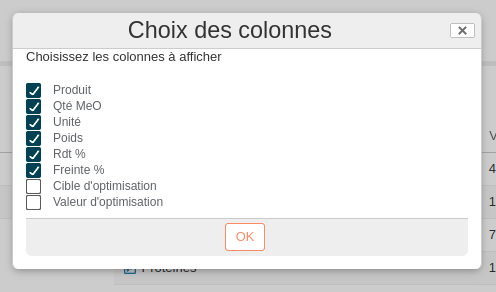
Il faut ensuite renseigner les différentes cibles de contrainte souhaitées pour chaque ligne dans la colonne "Cible d'optimisation". Une cible peut être :

• une valeur unique, ex: 58.2
• deux valeurs séparées par un point virgule ";", ex: 44;48, ce qui correspond à une valeur minimale et une valeur maximale (valeurs négatives acceptées)
• complétée par un nombre entre parenthèses, ex: 58.2 (10) ou 44-48 (15), ce qui va définir une valeur de tolérance pour cette cible exprimée en %
• vide, ce qui signifie que la ligne n'est pas considérée comme une contrainte

Il faut ensuite créer la formule SPEL qui va appeler le service GLOP pour effectuer le calcul.

Voici dans notre cas la formule utilisée (on souhaite minimiser le coût via l'argument target) :

var glopData = @glop.optimize({target: {var:  cost['workspace://SpacesStore/db597446-3458-405a-96d1-09b9593df1bb'], task: "min"}, constraints: {
               {list: compoList}, 
               {list: nutList}}});

setGlopData(#glopData);
glopData.getStatus();

Voici le résultat :

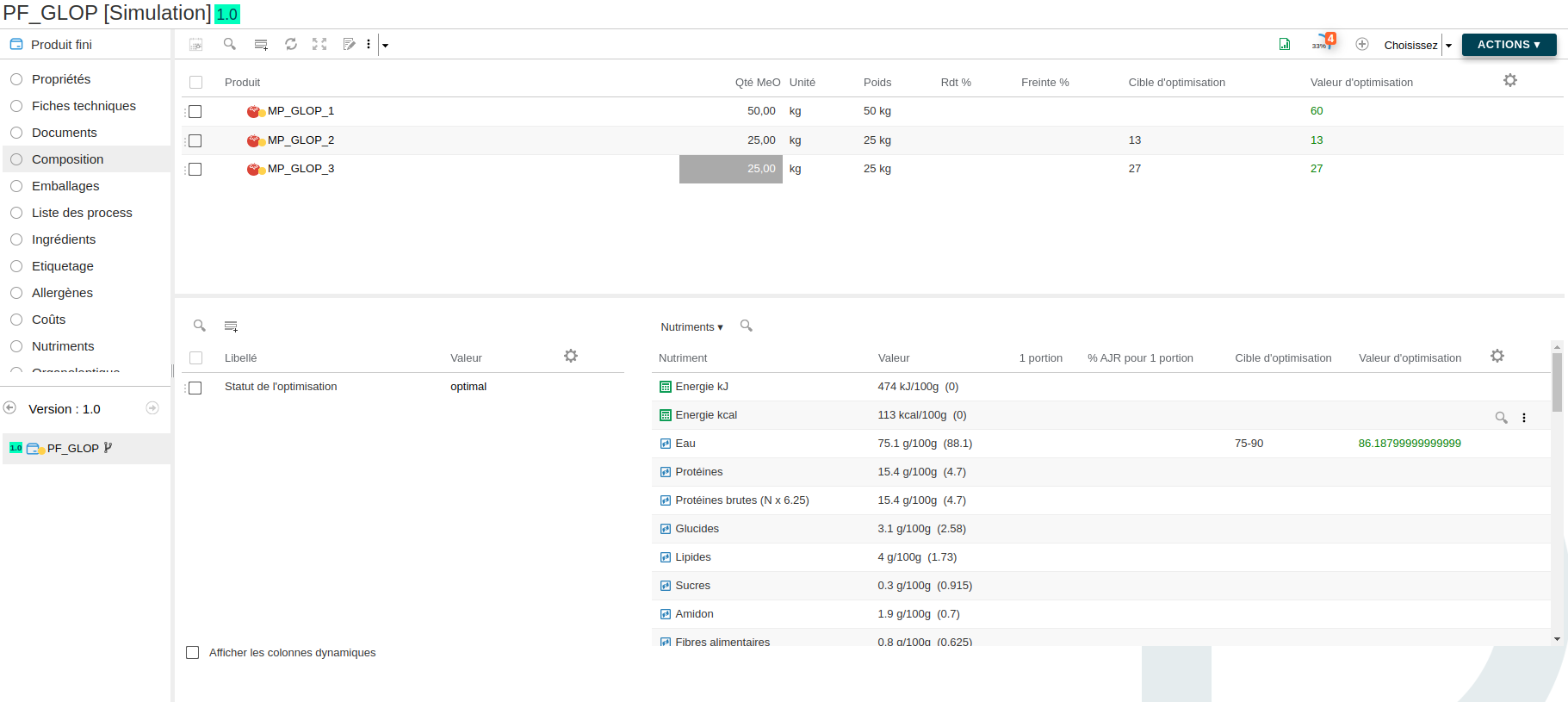
Ici on constate que le système a pu trouver une solution exprimée dans les colonnes "Valeur d'optimisation". Les valeurs sont en vert car elles sont comprises dans l'encadrement défini par leur cible respective.

Par défaut, le système cherche à résoudre le problème en conservant la quantité totale mise en oeuvre initiale dans le produit. C'est la raison pour laquelle les valeurs obtenues pour la composition ont pour somme totale 100 kg, la valeur totale initiale.

Il est possible de définir une contrainte sur cette valeur totale en ajoutant la ligne de contrainte

{var:"recipeQtyUsed", min:90,max:90}

Application de tolérances

Lorsque le système ne trouve pas de solution pour le problème, il est possible d'appliquer des tolérances (en %) sur les différentes contraintes.

• Soit depuis la formule SPEL : {list: compoList, tol:10} (ici, la tolérance est appliquée sur toute la liste)
• Soit depuis la colonne "Cible d'optimisation" : 6 (10) (ici, la tolérance est surchargée et appliquée sur la ligne uniquement)

Voici le réultat :

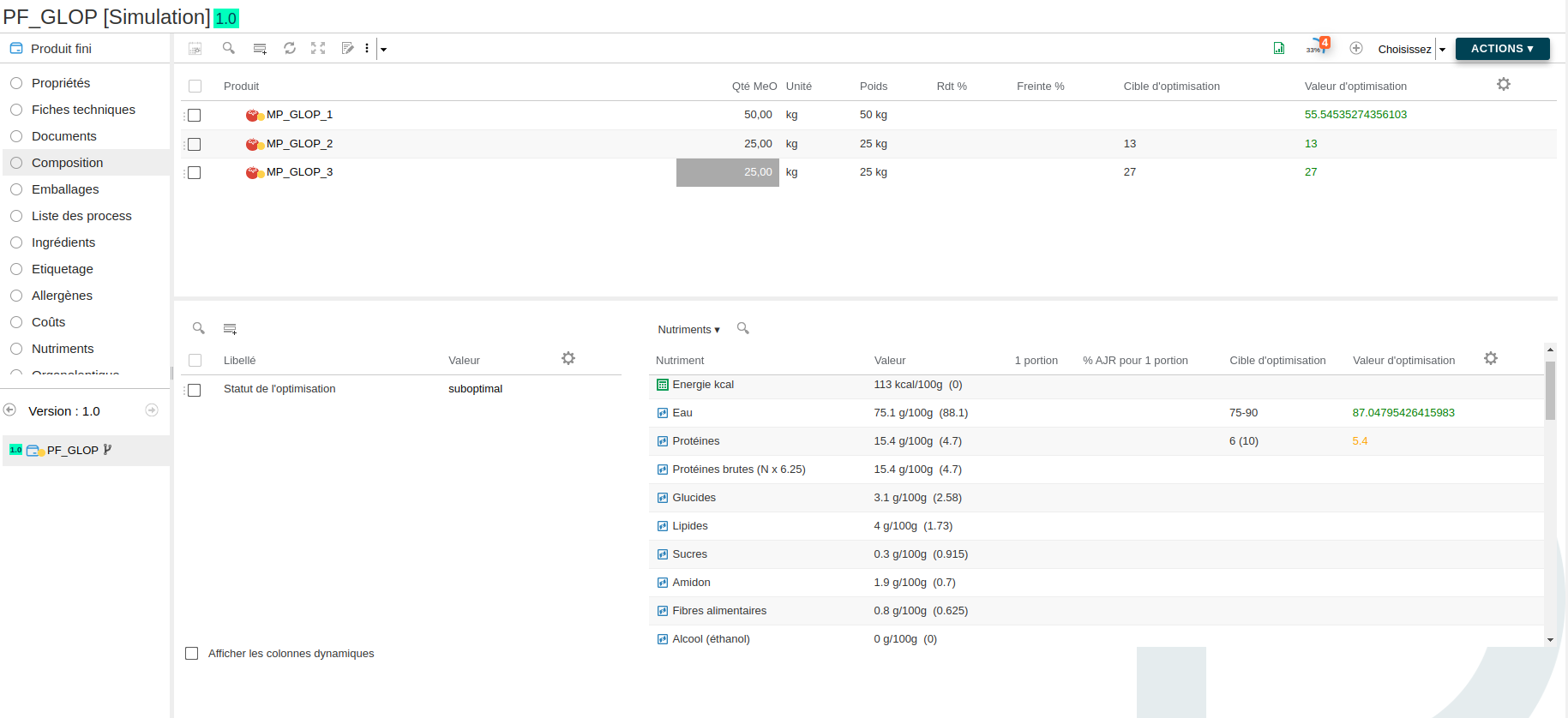
On peut constater la valeur d'optimisation "Protéines" est orange car le système a dû appliquer la tolérance de 10% pour trouver une solution.

Le statut de l'optimisation est alors "suboptimal".